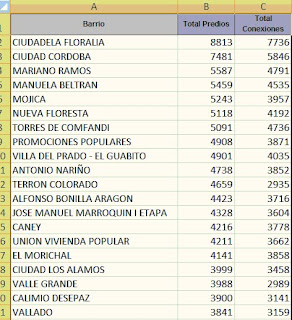
El primer paso es cuantificar el grado de relación lineal entre la cantidad de viviendas y el número de predios conectados al gas natural, para ello calculamos el Coeficiente de Correlación de Pearson.
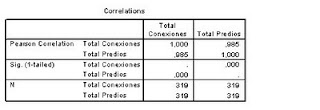
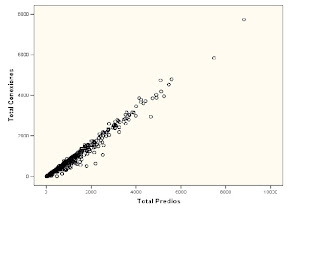
El coeficiente de Pearson nos dio 0.985 !!! se podría decir que existe una correlación lineal positiva casi perfecta. Se puede realizar un gráfico de dispersión para así comprobar la correlación, lo cual no esta mal, pero no es suficiente.
Entonces se procede ha plantear un modelo de regresión lineal simple, se ejecuta en el paquete SPSS y se obtiene el siguiente resultado.
Huy!!! un R cuadrado del 0.970 Muchos que trabajan datos adoptarian el modelo sin mas ni menos, pero cuidado.
En este momento cobran vida LOS SUPUESTOS ESTADÍSTICOS que son: de que para cada uno de los valores de la variable independiente la distribución de la variable dependiente debe ser normal. La varianza debe ser constante para la variable dependiente en cada uno de los valores de la variable independiente. La relación entre las variables X e Y debe ser lineal, y todos los valores observables deben ser independientes. Vamos ha ver algunos supuestos, aunque la labor del investigador es comprobar todos .
Normalidad:
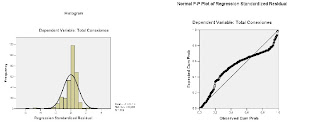
A simple vista el modelo no cumple el supuesto de normalidad ya los puntos de dispersión no siguen la linea recta, para comprobar esta hipótesis se realizo una prueba de Kolmogorff-Smirnov la cual se concluye de que no hay suficiente evidencia para aceptar la hipotesis de normalidad, además el comportamiento de la linea en S nos indica presencia de puntos atípicos los cuales provocan una distribución de los errores con alta curtosis de esta forma los estimadores mínimo cuadrados que son pocos eficientes o sea que la varianza del estimador es alta haciendo que la estimación sea menos fiable para solucionar este problema hay métodos como la regresión robusta o el método de mínimos cuadrados generalizados, este primero consiste en asignar menos peso a aquellos valores mas extremos.
Homocedasticidad:
Graficamente se observa que para el recorrido de la variable X la varianza del error no es constante (Heterocedasticidad), ya que esta tiene forma de embudo haciendo que los estimadores ya no sean eficientes o sea que su varianza sea alta
La solución y la comprobación de los otros supuestos estadísticos se escapa del objetivo de esta lectura pero existe suficiente bibliografia en donde se detalla muy bien la manera de llegar a un buen modelo, la idea de esta lectura es enfatizar de que no siempre un R cuadrado del 0.970 es bueno y que es solo es un pequeño paso para poder plantear un buen modelo. Igualmente considero que estos datos es un buen ejercicio para aquellos estudiantes que empiezan en el mundo de la estadística
para el que quiera comprobar por si mismo estos resultados me pueden escribir y a vuelta de correo les reenviare la base de datos.
Comentarios