Fácil y desde cero, Minería de datos. Aplicaciones casos reales. (Arboles)

Un banco quiere tener un modelo estadístico, en el cual permita medir el riesgo de realizar un préstamo hipotecario (pagos e impagos de la deuda), para poder cuantificar este riesgo se va a tener en cuenta una serie de variables que según el científico de datos puede llegar a ser relevantes.Para esto se selecciona una muestra representativa de la población de usuarios del banco. Los datos describen el comportamiento de cada cliente al corte de un periodo dado, de tal manera que se tendrá dentro de la muestra personas que están al día  o en mora con su crédito hipotecario.

A continuación se realizará una descripción de las variables que quizás puedan influenciar en el resultado del modelo.

En resumen, son variables que indican numero de obligaciones, en diferentes cortes de tiempo, cantidad de consultas a la centrales de riesgo, porcentajes de deudas, saldos de deudas, tiempos trascurridos desde el ultimo pago etc ...

Siguiendo la metodología de minería de datos lo primero que se realiza es una preparación y análisis descriptivo de los datos, para ello se utilizará el SAS ENTERPRISE MINER 14.2.

1. Lo primero que se va a hacer es crear un proyecto llamado Prueba. la ruta es: Archivo>Nuevo>Proyecto...
   
2. En el paso 2 de 4 se le asigna el nombre. Prueba
   
3. Se le da siguiente hasta finalizar en el paso 4.
4. Luego se creará un diagrama llamado Sección1. la ruta es: Archivo>Nuevo>Diagrama...
   
5. Al definir un diagrama de trabajo se procede a importar la metadata, para lo cual se recomienda trabajar desde una librería de datos, la cual pudo haber sido creada por el administrador, o por el usuario.
   
6. En el paso 5 de 9, se procede a hacerle los siguientes cambios a la metadata.
   
7. Se le da siguiente hasta finalizar la importación de los datos. Quedando el proyecto de la siguiente manera:
   
8. Igualmente nos aseguramos con trabajar los la totalidad de los datos. Opciones>Preferencias...
   

En el siguiente video se analiza la forma en la cual se crea un proyecto:

Examinando Valores perdidos en la data:

Para ver los valores vacíos en la base de datos se procede a utilizar el nodo de exploración de datos, tal como se ve a continuación:

Al abrir los resultados (Interval Variable Summary Statistics) se puede observar que se tiene al rededor de 11 variables con valores perdidos:

Examinando la distribución de las variables:

Dentro del explorador de estadísticos igualmente se puede mirar el sesgamiento positivo, negativo o sin sesgo de las variables. lo cual se hace comparando la media (Me) y la mediana (Md), de tal forma que si 

• Me > Md entonces sesgo positivo.
• Me < Md entonces sesgo negativo.
• Me = Md entonces sin sesgo.

Por otro lado también se puede ver la Skewness (Sk) si:

• Sk es positiva el sesgo es positivo.
• Sk es cero no hay sesgo.
• Sk es negativo el sesgo es negativo.

Por ejemplo para la variable InqTimeLast.

Esta variable tendría una distribución positiva.

Asociación entre variables independientes y variable dependiente:

Igualmente es importante analizar las posibles asociaciones que pueden existir entre variables independientes, para lo cual se hace uso del estadístico chi-cuadrado, este valor se puede ver de forma gráfica y numérica, donde se proporciona el estadístico junto con el valor p.

Tal como se observa un chi cuadrado alto es inversamente proporcional al valor p recordemos que el valor p se puede interpretar como la probabilidad de que la hipótesis nula (independencia entre variables) sea cierta, por ende podemos decir que existe dependencia o relación entre la variable dependiente y  las siguiente variables  independientes: (TLDel60Cnt24, TLDel90Cnt24, TLDel3060Cnt24, TLBadCnt24, TLCnt12).

Analizando el apuntamiento de la distribución de las variables:

Para evaluar el nivel de apuntamiento de cada una de las distribuciones, se procede a mirar los resultados del nodo de explorador de estadísticos.

recordando que si:

• Kurtosis > 0  es Leptocurtica
• Kurtosis = 0  es Mesocurtica
• Kurtosis < 0  es Platicurtica

Con esta información podemos decir que:

La gran mayoría de variables son Leptocurticas o sea que su indicador de apuntamiento es mayor a cero.

Análisis de variables independientes categóricas vs variable independiente:

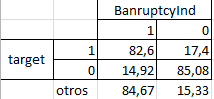
Este análisis es importante por que podemos ver el peso de cada una de las categorías de la variable independiente frente a la variable dependiente. El programa da las siguientes salidas al respecto.

lo cual se puede extrapolar a:

"De tal manera que un 14,92 % de los clientes que no han pagado su crédito hipotecario  están en Bancarrota."

En el siguiente video a manera de complemento se explica con otros datos, la manera en la cual se hacen análisis descriptivos de la información:

Trasformación de Variables:

En muchas ocasiones se debe de hacer trasformaciones de variables o creación de nuevas a partir de otras. Este procedimiento es útil cuando se quiere estabilizar varianza, eliminar no linealidad, corregir la normalidad y de una forma generar que los datos de ajusten mas a un modelo predeterminado.

Por defecto las variables intervalo independiente,  como las demás, no tienen tipo de transformación. 

Imputación de Variables:

Las bases de datos de minería de datos a menudo contienen observaciones que tienen valores faltantes para una o más variables. Los valores que faltan pueden resultar de errores de recopilación de datos, respuestas incompletas del cliente, fallas reales del sistema y de mediciones.

Si una observación contiene un valor faltante, entonces por defecto esa observación no se usa para modelar por nodos tales como Red Neural, o Regresión. Sin embargo, rechazar todas las observaciones incompletas puede ignorar la información útil o importante que aún está contenida en las variables no faltantes. Rechazar todas las observaciones incompletas también puede sesgar la muestra.

¿Cómo se deben tratar los valores de datos perdidos? No hay una sola respuesta correcta. La elección de la "mejor" técnica de reemplazo de valor faltante requiere inherentemente que el investigador haga suposiciones sobre los datos verdaderos (faltantes). Por ejemplo, los investigadores suelen reemplazar un valor perdido por la media de la variable. Este enfoque supone que la distribución de datos de la variable sigue una distribución normal de la población. La sustitución de los valores faltantes por la mediana, la mediana u otra medida de tendencia central es simple, pero puede afectar en gran medida la distribución de la muestra. Debe utilizar estas estadísticas de sustitución cuidadosamente y sólo cuando el efecto es mínimo.

Otra técnica de imputación reemplaza los valores faltantes con la media de todas las demás respuestas dadas por la fuente de datos. Esto supone que la entrada de esa fuente de datos  se ajusta a una distribución normal. 

Por ahora y como ejercicio vamos a realizar una imputación a una variable, para lo cual vamos a conectar el nodo imputación a los datos y a dirigirnos a a las propiedades del nodo, en el item de variables, allí podemos configurar para la variable TLSum el método de imputación del Árbol.

Para ver los estadísticos de la variable imputada, se debe hacer lo siguiente:

De esta forma podemos mirar como han cambiado los estadísticos, cuando se aplican las trasformaciones.

Nodo de re emplazamiento:

En algunos casos, es posible que desee reasignar algunos valores  de tal manera que por ejemplo se recorte de la distribución de una variable. Por ejemplo, esto se aplicaría para una con la distribución bimodal.

Es posible que desee recortar de un lado de la distribución para crear una distribución más estricta y centralizada  antes de imputar valores perdidos, por ende se recomienda utilizar un nodo de reemplazo antes de un nodo de imputación.

El nodo de reemplazo debe de seguir un nodo que exporta un conjunto de datos, tales como un nodo Origen de datos, Muestra o Partición de datos.

de igual forma podemos realizar reemplazos por variable, tal como se observa en la siguiente gráfica:

Partición de datos: El particionamiento proporciona conjuntos de datos mutuamente excluyentes. Dos o más conjuntos de datos mutuamente exclusivos donde ninguno de los grupos no comparten ninguna observación entre sí. La partición de los datos de entrada tiene la ventaja de reducir el tiempo de cálculo de las pruebas preliminares de modelado. Sin embargo, se debe tener en cuenta que para conjuntos de datos pequeños, el particionamiento puede ser ineficiente, ya que el tamaño reducido de la muestra puede degradar el ajuste del modelo y su capacidad para generalizar.

¿Cuáles son los pasos para particionar un conjunto de datos? Primero, se especifica un método de muestreo: muestreo aleatorio simple, muestreo aleatorio estratificado o muestreo por conglomerados. Como segundo paso, se especifica la proporción de observaciones muestreadas para así poder escribir cada conjunto de datos de salida (entrenamiento, validación y prueba). No es raro omitir el conjunto de datos de prueba y no asignarle ninguna cantidad de datos.

en este caso vamos a asignar los siguientes: 

• Entrenamiento = 60%
• Validación = 30%
• Prueba = 10%

Por ejemplo podemos ver la cantidad de registros que están en modo impago para el conjunto de validación.

Video Explicativo Partición de Datos:

Arboles de decisión: 

Un árbol simple representa una segmentación de los datos que se crea mediante la aplicación de una serie de simples reglas. Cada regla asigna una observación a un segmento basada en el valor de la variable independiente. Una regla se aplica después de otra, dando lugar a una jerarquía de segmentos dentro de otros segmentos. A esta jerarquía se le llama árbol, y cada segmento se le llama nodo. El segmento original contiene el conjunto de completo datos  y se denomina nodo raíz del árbol. Un nodo con todos sus sucesores forma una rama. Los nodos finales se llaman hojas. Para cada hoja, se toma una decisión y esta se aplica a todas las observaciones en la hoja. El tipo de decisión depende del contexto, en el que el modelo predictivo, se presenta.

El Árbol de decisión se utiliza  para las siguientes tareas:

• Clasificar las observaciones basadas en los valores de las variables objetivo nominales, binarios u ordinales.
• Pronosticar resultados en función de las variable dependientes.

Una ventaja del modelo de árbol de decisión sobre otros modelos, como la red neuronal, es que produce salida que describe el modelo de puntuación con reglas interpretables. El modelo de Árbol de decisión también produce salida de código de partitura detallada que describe completamente el algoritmo de puntuación en detalle. Por ejemplo, las Reglas de un modelo podrían describir las reglas: 

"Si la proporción mensual de la hipoteca sobre el ingreso es menor al 28% y los meses de mora son  0 y el salario es mayor de $ 30,000, entonces emita una tarjeta de crédito tipo Gold".

Otra ventaja del modelo Árbol de decisión es el tratamiento de los datos que faltantes. Dado que se puede utilizar una regla de división que permita identificar los valores nulos de una variable. Igualmente las reglas de sustitución están disponibles como respaldo cuando los datos perdidos prohíben la aplicación de las reglas de división.

Nota: Las reglas de un nodo son útiles para entender la estructura de un árbol de decisiones. Sin embargo, no se recomienda usar las Reglas de un solo nodo como una única base para un algoritmo de puntuación. 

Los árboles de decisión producen un conjunto de reglas que pueden usarse para generar predicciones para un nuevo conjunto de datos. Esta información que se obtiene puede utilizarse para impulsar las decisiones empresariales. Por ejemplo:

"En el marketing de bases de datos, los árboles de decisión se pueden utilizarse para desarrollar perfiles de clientes que ayuden a los vendedores a orientar los envíos promocionales para generar una mayor tasa de venta".

La implementación de árboles de decisión se encuentran divisiones multidireccionales basadas en el tipo de variables independientes nominales, ordinales y de intervalo. También podemos elegir los criterios de división de cada nodo y por ultimo el método de construcción del árbol. entre las cuales se destacan por su popularidad:

CHAID (detección automática de interacción Chi-cuadrado) y las descritas en Árboles de Clasificación y Regresión. (Véase L. Breiman, J.H. Friedman, R. A. Olsen y C. J. Stone, 1984.)

Por otro lado, las probabilidades previas y las frecuencias le permiten al científico de datos utilizar los datos de entrenamiento en diferentes proporciones. Por ejemplo, si el fraude ocurre en el 1% de las transacciones, entonces una décima parte de los datos de no fraude suele ser suficiente para desarrollar el modelo.

El criterio para evaluar una regla de desdoblamiento puede basarse en una prueba de significancia estadística (a saber, una prueba F o una prueba de Chi cuadrado) o en la reducción de la varianza, entropía o medida de impurezas de Gini. La prueba F y la prueba Chi-cuadrado aceptan a una variable con el valor p como regla de detención. Todos los criterios permiten la creación de una secuencia de subárboles. Las cuales puede utilizarse en los datos de validación para seleccionar el mejor subárbol.

Se podría analizar la probabilidad de la no ocurrencia del evento por cada uno de los clientes que toman un crédito de vivienda, para lo cual se analizará específicamente:

"para el cliente id=000355 cuyo registro se encuentra el la tabla de entrenamiento, por lo tanto se tiene una probabilidad de no pagar el crédito del 0.0659 o 6,6%"

Se puede mirar fácilmente, a partir de los resultados, el nivel de importancia de la variables que aportan al modelo:   

De donde podemos ver cuales son las variables que más peso predictivo y de clasificación que tiene las variables dentro del modelo:

Se observa que alrededor 6 variables son importantes dentro del modelo.

"La variable mas importante para definir un préstamo será aquella con la cual se hace el primer nodo, por ende será el numero de lineas de crédito."

El numero de reglas de segmentación indica las veces en las cuales las variables aparecen como nodo en el diagrama del árbol de decisión.

El programa también proporciona el valor de la importancia de las variables en el conjunto de datos de entrenamiento como los de validación, junto con la diferencia porcentual entre estos dos indices.

También se puede medir el nivel de ajuste de los datos al modelo, para lo cual se hace uso de estadísticos de ajuste entre los cuales están el misclassification rate,  este estadístico se recomienda verse en el conjunto de datos de prueba o por su defecto en el grupo de validación.

 Acá se analiza el % de mala clasificación del modelo o sea la suma de los falsos positivos y los falsos negativos,  estos se obtiene cuando se confronta los resultados del modelo y los valores reales. Se esperaría que el valor del indicador converga a cero, 

"sin embargo un valor de 0.168, se considera como un bueno, esto por que  tan solo el modelo clasifica mal el 16,8% de los datos,"

igualmente se recomienda profundizar un poco mas en este indicador y analizar por aparte los falsos positivos y los falsos negativos. 

En el siguiente cuadro procedemos a analizar las frecuencias y las proporcionalidades en cuanto al total general y a los totales marginales de la variable respuesta real.

lo cual se puede extrapolar de la siguiente manera:

"Por ejemplo podemos identificar un problema del pronostico que hace el árbol, por ejemplo los clientes que no han pagado su hipoteca  están siendo pronosticados de manera incorrecta, esto por que el modelo los clasifica como buenos pagadores, lo cual es un problema para un Banco."

Acá un vídeo explicativo de los arboles:

Cualquier duda o información adicional me pueden escribir o contactar, e indicarme sobre que tema quisieran que profundice.